個人的な主観ですが、一番の難関は分数かと思っていますが・・・?
実際の所どうなのでしょうか?
大学生で分数ができない時点で・・・?
都市伝説かと思ったら、ホントだった件。
分数が分からない大人がいる事。
1/4+1/3が 2/7になるというミラクル。
実際は3/12+4/12=7/12 が正解なのですが・・・。
通分という概念を理解してないと一生かかっても解けません。
計算の順序が分からない
足し算引き算掛け算割り算の順番がカオスになる人。
加減乗除を理解していれば何てことはないのですが・・・。
10+2×5=?
12×5=60 不正解
10+10=20 正解
掛け算割り算を優先
10+2×4÷2=?
掛け算割り算を優先していれば
どちらからやっても問題なし。(括弧がある場合を除く)
2×4をして2で割ろうが
4÷2をしてから2で掛けようが答えは一緒です。
答えは14です。
この2つについての質問や悩みが特に多いように感じました。
ただ
この2つは基本中の基本で理解しないままでいると、
大人になっても分からない状況になります。
習った瞬間から、理解することがつまづかない要因になります。
最初の助走というか、習いたてで、しっかりと覚えるのが大切です。
では どうやって理解させるべき?
分数の場合、通分という概念をどうやって教えるかがポイントだと思います。
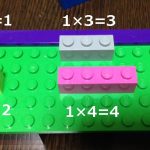
私のアイデアですが、レゴを使うやり方を思いつきました。
コチラにまとめたので参考にしてください。
計算の順序に関しては、足し算と引き算が仲間。
掛け算と割り算が仲間という事を理解出来ればOKでしょう。
足し算と引き算だけの式なら、どう解こうが、答えは一緒です。
同じように
掛け算と割り算だけの式も、どう解こうが答えは一緒です。
これが理解出来れば、計算順序も理解できるハズです。
と思ったら足し算掛け算割り算引き算が混ざった計算って
中学校から習うらしいですね・・・。知りませんでした。
ただ、小学校のうちに
足し算と引き算が仲間で、掛け算と割り算が仲間という事を
理解していれば、中学でつまづく事は無いと思います。
難関は、やはり分数ですね。