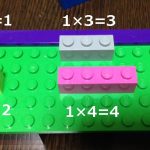
レゴのブロックを利用して分数が理解できるかも。
1/4と1/2をブロック等で再現してみると、わかるかも知れない。
通分の概念をレゴに置き換えると?
まずはレゴで3分の1と2分の1を再現してみました。
下のブロックが分母を表現して
上のブロックが分子を表現しています。
3分の1

3分の1を表現したものです。
下のブロックがポッチ3のブロックで分母を
上のブロックがポッチ1で分子を表現しています。
2分の1

同じようにポッチ2のブロックで分母を
ポッチ1のブロックで分子を表現しています。
1/2+1/3→?

分母があっていません。これを合うまで
それぞれに同じブロックを並べていく必要があります。
これが通分の概念となるのです。

1/2の方は 同じブロック3つ
1/3の方は 同じブロック2つで分母を合わせることが出来ました。
それぞれポッチが6個になっています。分母が6ということが分かります。

3/6+2/6=5/6で6分の5になりました。
分数の足し算はこのようになります。